今天要講的資料結構叫做Graph，中文稱作圖，Graph是一個相對廣泛概念並且能夠應用在很多日常生活情境的資料結
構。

我們來看看Graph長怎麼樣。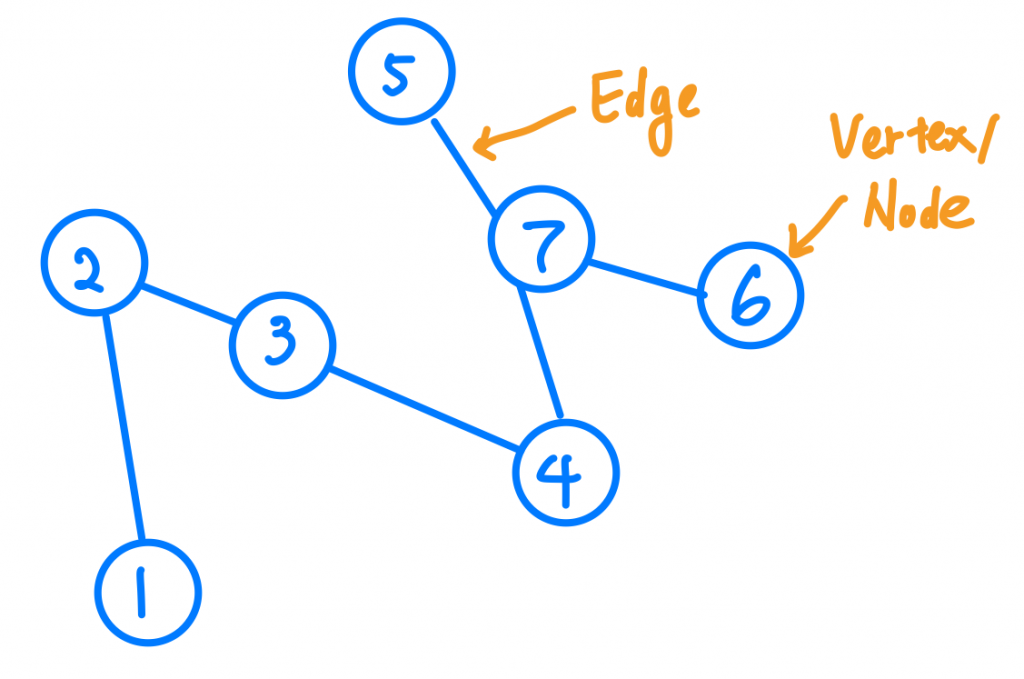

我們可以發現Graph是由節點跟邊組成的，節點我們稱作Node或Vertex，邊我們稱做Edge。

我們可以更進一步的說這個圖是一個「無向圖」，意思就是，每一個邊都沒有方向性。我們說到無向，那就一定會有「有向圖」了，沒有錯，有向圖就是長這樣子的啦。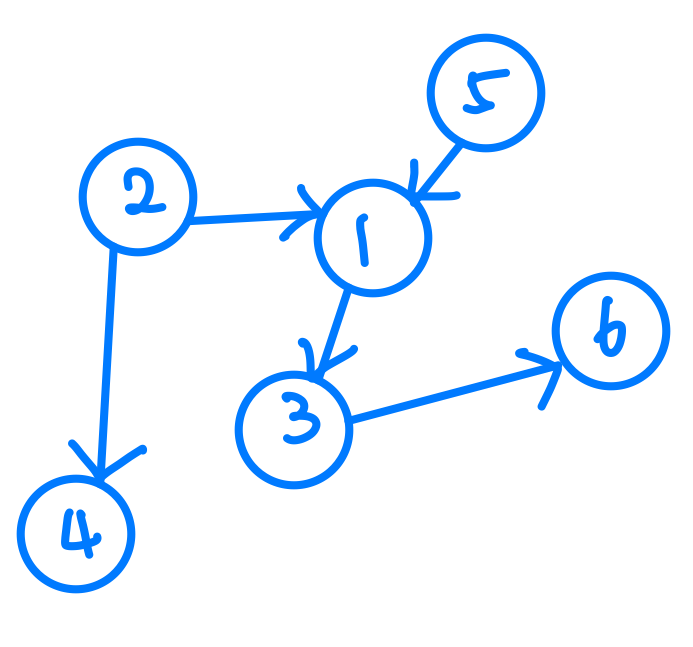

以下我想用一些生活化的例子來解釋有向跟無向的差別，首先我們先看看instagram這類型的社交網路我們可以發現，你可以單向的追蹤明星，它不一定要追蹤你。那我們反過來看看Facebook這類型的社交網路，我跟你成為朋友後，我就是你朋友，你也就是我朋友，意思其實就是我們是沒有任何方向性的(雖然新功能是可以單向追蹤，我們先不用理會這種情況)，或者你要說都是雙向性的。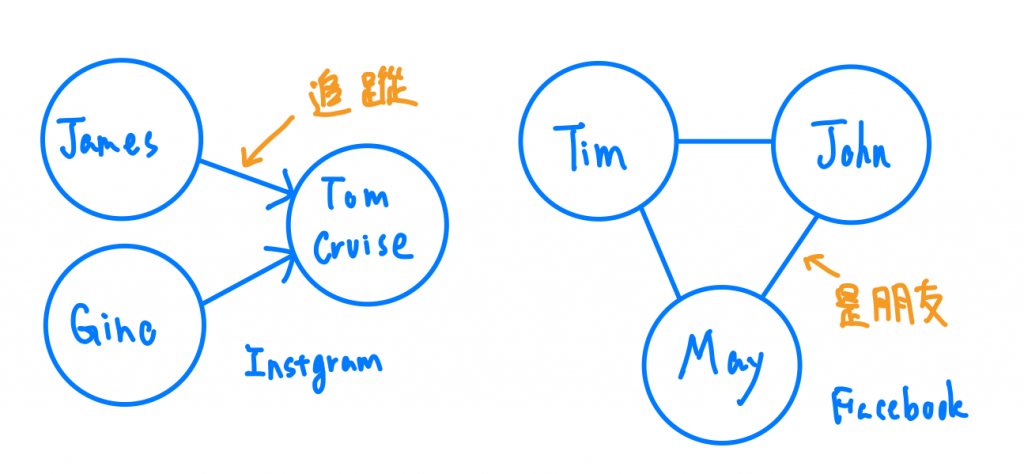

圖的表示法

圖有最常見的兩種表示法，一種是相鄰串列，一種是相鄰矩陣，我個人是比較偏好使用相鄰串列，不過概念上都是可以互通的，如果對相鄰矩陣，有興趣的同學可以去上網查看看相關的文章喔！那我們就來看看有向圖跟無向圖怎麼用相鄰串列來分別表示他們吧！

有向圖在Pyhton裡的表示法

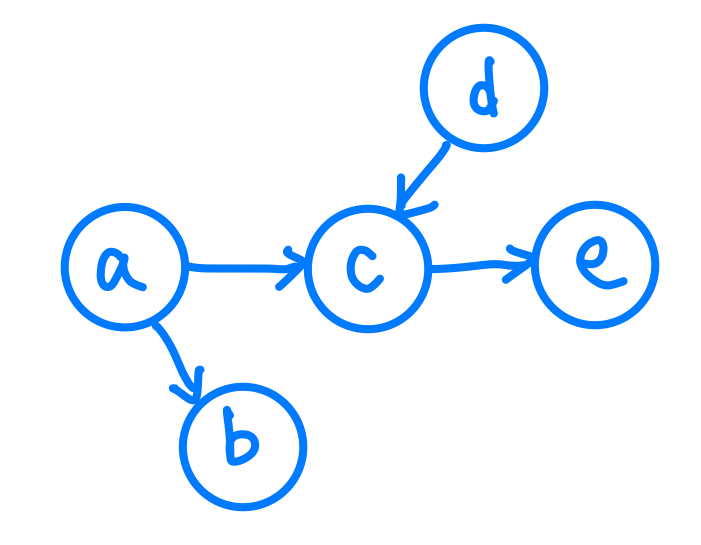
graph = {
    'a':['b', 'c'],
    'b':[],
    'c':['e'],
    'd':['c'],
    'e':[]
}

無向圖在Pyhton裡的表示法

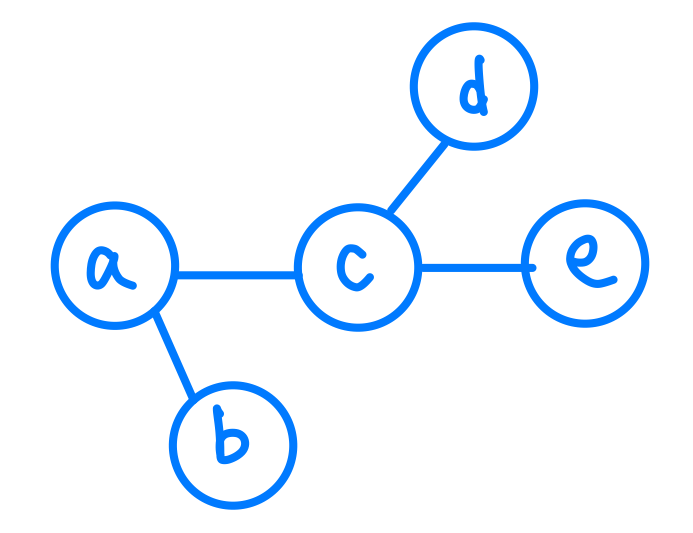
graph = {
    'a':['b', 'c'],
    'b':['a'],
    'c':['a', 'd', 'e'],
    'd':['c'],
    'e':['c']
}

我們可以發現在無向圖裡面，如果a跟b之間有Edge那麼b就會在a的list裡，a也會在b的list裡面。而在有向圖裡頭，a指向b，就只會有b在a的list裡而已。

另外圖也有另一個特性，就是有沒有圓圈，如果有我們會稱之為有環，沒有的話我們會稱之為無環，再把剛剛我們講到的有向無向概念加進去，這樣就會有四種組合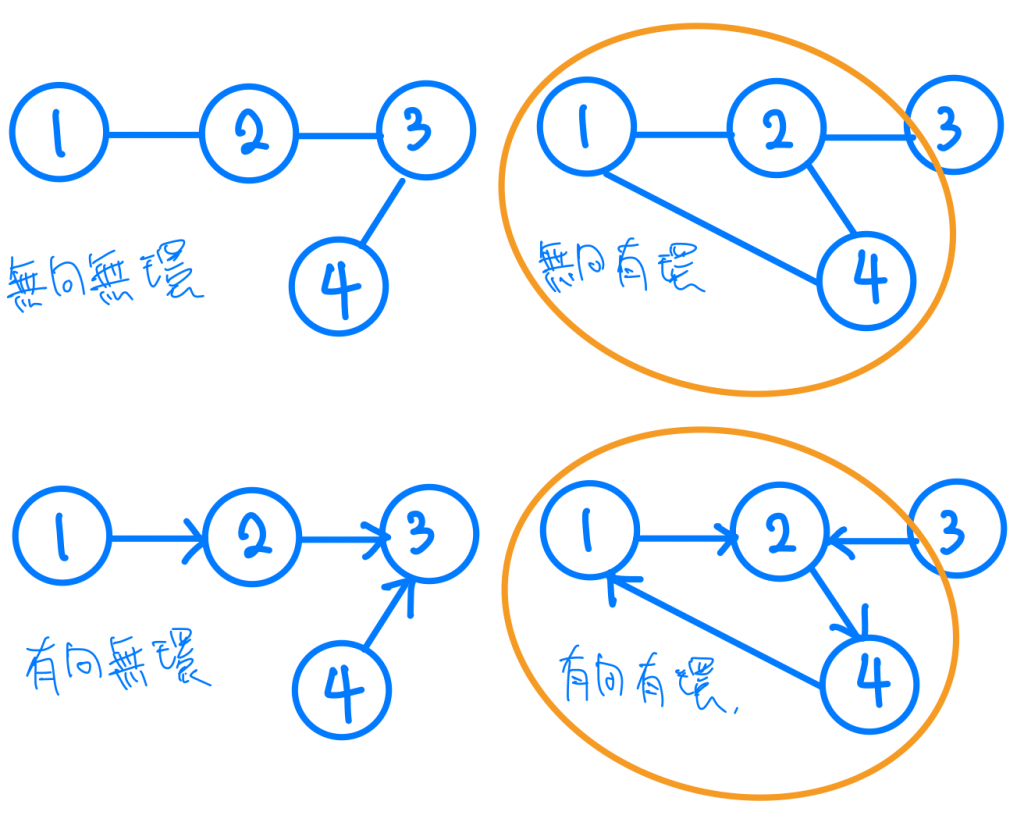

從樹到鏈結串列

眼尖的讀者們可能已經發現了，樹就是一種特別型態的圖，更精確的說，樹是一種特別的有向無環圖，而Link List是一種很特別的樹，可以想像只有樹的右邊有值。現在再試著回想我們前面所提到的資料結構重點是在於它的「概念」，而不是它是怎麼實作，是不是又更有一點感覺了呢？